哈尔滨学院
课程思政教学案例
课程名称:高等数学A2
授课教师:李明哲
课程类型:专业教育课程
课程性质:必修
案例个数:5
案例1:常数项级数的概念和性质
一、基本信息
课程名称
|
《高等数学》A2
|
授课教师/职称
|
李明哲、徐亚兰、毕淑娟、曹辉/副教授;
朱莉、盛晓娜、王永红/讲师
|
课程类型
|
专业教育课程
|
课程性质
|
þ必修 ¨选修
|
案例学时/总学时
|
2/160
|
授课对象及人数
|
计算机、软件工程、土木、城地20级/470人
|
教学方式
|
¨线下 ¨线上 þ线上线下混合式
|
二、案例设计
本次课程目标:
1. 掌握常数项无穷级数及其敛散性的概念。
2. 熟练掌握无穷级数收敛性的判定。
3. 掌握收敛级数的性质。
思政育人目标:
1.介绍无穷级数的历史和起源,展示数学之美,特别介绍我国古代数学家的卓越贡献,培养科学的历史观,增强学生的自信心和民族自豪感。
2. 从级数理论中深入挖掘和谐元素,让学生在数学理论学习中感受和谐之美和审美情操的熏陶。
3. 通过专业知识的深入讲解,扩大学生的视野,提高学习兴趣。
4. 培养学生的动手能力,加强学生对专业数学知识的应用。
|
案例教学
内容
|
§ 12.1 常数项级数的概念和性质
一、常数项级数的概念
定义1 给定一个数列
 , 则由这数列构成的表达式 , 则由这数列构成的表达式
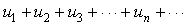 叫做(常数项)无穷级数, 简称级数, 记为 叫做(常数项)无穷级数, 简称级数, 记为
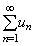 , 即 , 即
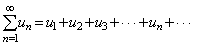 , 其中第n项u n 叫做级数的一般项. , 其中第n项u n 叫做级数的一般项.
二、常数项级数的敛散性概念
定义2 级数
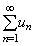 的前n项和 的前n项和
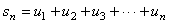 ,称为级数 ,称为级数
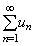 的部分和。这是有限项的和,当 的部分和。这是有限项的和,当
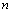 依次取 依次取
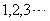 时,他们构成了一个新的数列 时,他们构成了一个新的数列
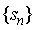 ,称为部分和数列。 ,称为部分和数列。
根据部分和数列是否有极限,我们引进无穷级数敛散性的概念。
定义3 如果级数
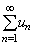 的部分和数列 的部分和数列
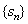 有极限s, 即 有极限s, 即
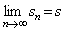 , 则称无穷级数 , 则称无穷级数
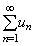 收敛, 这时极限s叫做这级数的和, 并写成 收敛, 这时极限s叫做这级数的和, 并写成
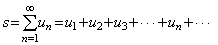 ; 如果 ; 如果
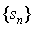 没有极限, 则称无穷级数 没有极限, 则称无穷级数
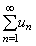 发散. 此时这无穷多个数相加是没有和的。 发散. 此时这无穷多个数相加是没有和的。
定义4 当级数
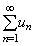 收敛时, 其部分和s n是级数 收敛时, 其部分和s n是级数
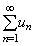 的和s的近似值, 它们之间的差值rn=s-sn=un+1+un+2+ × × × 叫做级数 的和s的近似值, 它们之间的差值rn=s-sn=un+1+un+2+ × × × 叫做级数
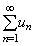 的余项。 的余项。
三、常数项级数的敛散性的判定
例1 判别无穷级数1+2+3+× × ×+n+× × ×的收敛性。
例2 判别无穷级数
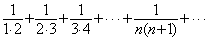 的收敛性。 的收敛性。
例3证明调和级数
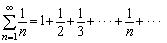 发散。 发散。
例4 讨论等比级数(几何级数)
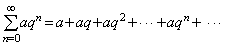 的敛散性, 其中a¹0, q叫做级数的公比。 的敛散性, 其中a¹0, q叫做级数的公比。
|
思政要素
切入点
|
1. 展现数学史全貌,增强学生的民族自豪感。
在讲解级数概念时,把同学们带回到无穷级数这段数学史的起点,从我国古书中最早的关于无穷级数的数学思想讲起,介绍三国的刘徽、北朝的祖冲之,说明中国人是世界上最早发现、最早研究圆周率的国家之一,带领同学们了解数学历史全貌。
2. “如盐入味”,把育人元素自然融入到专业知识的教学。
在讲解调和级数的发散时,调和级数的通项趋近于0,但是级数本身却发散到∞,这个数学结果告诉我们一个深刻的道理,不要小看少量的积累,很多小量的加和可以很大,正如习近平总书记谈教育的金句:每个人的生活都是一件件小事组成的,养小德才能成大德。古训“不以善小而不为,不以恶小而为之” 说的也是这个道理。
在当下“战疫”的特殊时期,每名同学曾经响应国家号召,在疫情封闭状态下努力学习,遵守疫情的各项规定,看似微不足道,但是全国人民众志成城,最终取得了举世瞩目的成就;反之,如果个别同学放松防控,一旦蔓延开来,我们的努力就会功亏一篑。
3. 注重教学知识深入化、应用性。
讲完调和级数的发散,进一步深入介绍调和级数的阶估计,引入Euler 常数,同时介绍大数学家Euler在应用数学方面的贡献,进一步激发学生的学习热情。
|
教学策略
|
结合使用案例教学法、对分教学和混合式教学。
|
三、案例实施
一、实施过程
1.学习级数概念,从公元前300年我国著名哲学家庄周所著的《庄子·天下篇》里关于无穷级数的数学思想讲起,自然的引出无穷级数及其收敛的概念。

2.再谈到魏晋时代,数学家刘徽应用无穷级数的概念来计算圆的面积,发明割圆术,比西方早了一千多年。
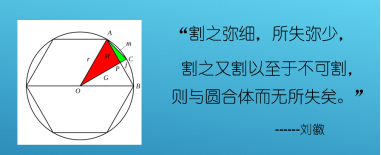
刘徽最早得到逼近圆周只需要计算圆内接正多边形面积的方法,利用割圆术得出精确到小数点后2位的π值.
祖冲之利用割圆术进一步得出精确到小数点后7位的
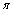 值(公元466年)这一记录在世界上保持了一千年之久。 值(公元466年)这一记录在世界上保持了一千年之久。
3.在证明调和级数
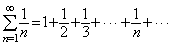 的发散性时,虽然调和级数的通项趋近于0,但是调和级数本身却发散到∞。引申出一个深刻的道理:不要小看少量的积累,很多小量的加和可以很大,正如习近平总书记谈教育的金句:每个人的生活都是一件件小事组成的,养小德才能成大德。古训“不以善小而不为,不以恶小而为之” 说的也是这个道理。 的发散性时,虽然调和级数的通项趋近于0,但是调和级数本身却发散到∞。引申出一个深刻的道理:不要小看少量的积累,很多小量的加和可以很大,正如习近平总书记谈教育的金句:每个人的生活都是一件件小事组成的,养小德才能成大德。古训“不以善小而不为,不以恶小而为之” 说的也是这个道理。


4.介绍调和级数与自然对数的差,再取极限,由此得到Euler 常数c的定义。
同时介绍大数学家Euler,欧拉是18世纪数学界最杰出的人物之一,几乎每一个数学领域都可以看到Euler的名字。他不但在数学上作出伟大贡献,而且把数学用到了几乎整个物理领域。用科学家的事迹进一步激发学生的学习热情,特别是应用数学解决其他领域问题的热情。布置开放式作业,让同学们课后查找资料,整理无穷级数的数学史及Euler常数的应用。进一步打开学生的视野,培养学生的科研能力。
二、取得成效
1.学生形成 “爱数学,学数学,做数学” 的良好风气。
2.学生对相关数学史有了深入了解,形成科学的历史观,激发强烈的民族自豪感,增强祖国科技振兴的信心。
3.思政引导形象具体,学生对专业知识有了透彻的认识,印象十分深刻,极大促进专业知识的学习。
4.学生铭记“养小德才能成大德”,凡事要从平时的一点一滴做好,也坚定了在疫情封闭状态下刻苦学习的信念。
5.通过教学知识的深入化和割圆术的介绍,学生加深了数学的应用能力,学习兴趣大增。
三、教学反思
刘徽的割圆术多数学生有所了解,可以让学生来具体讲解,效果更生动。本节课的教学设计,恰到好处地找到了德育元素和教学内容的契合点,而不是为了德育而德育,为了思政而思政,生搬硬套,牵强附会。在不能改变以知识传授为主的传统教学方式前提下,树立了新颖的教学思维,让融化在数学中的德育元素成为学生求学、做人、做事的动力源泉。
|
案例2:定积分的概念与性质
一、基本信息
课程名称
|
《高等数学》A2
|
授课教师/职称
|
李明哲、徐亚兰、毕淑娟、曹辉/副教授;
朱莉、盛晓娜、王永红/讲师
|
课程类型
|
专业教育课程
|
课程性质
|
þ必修 ¨选修
|
案例学时/总学时
|
2/160
|
授课对象及人数
|
计算机、软件工程、土木、城地21级/485人
|
教学方式
|
þ线下 ¨线上 ¨线上线下混合式
|
二、案例设计
本次课程目标:
1.掌握定积分的概念。
2.掌握定积分的性质。
3.理解定积分的几何意义 。
思政育人目标:
1.本节在介绍定积分概念时,通过求曲边梯形的面积实例总结出定积分的定义,引入以平代曲的辩证哲学思想,激发学生的学习兴趣,培养学生的应用意识和解决实际问题的能力。
2.定积分的数学思想可以概括为分割(化整为小)、作积(局部近似)、求和(化小为整)、取极限(精确化),启发学生再复杂的事情都是由简单事情组合起来的,利用这一思想在遇到困难时可以将大问题切割成小问题来解决,培养学生分析问题和解决问题的能力。
3.在讲授定积分的概念和性质时,将不定积分和定积分的概念进行对比,使学生发现其中蕴含的矛盾对立统一、普遍联系和否定之否定的辩证哲学规律。
|
案例教学
内容
|
§5. 1 定积分概念与性质
一、实例
1.求曲边梯形的面积
曲边梯形: 设函数y=f(x)在区间[a, b]上非负、连续. 由直线x=a、x=b、y=0及曲线y=f (x)所围成的图形称为曲边梯形。
思想方法:以平代曲。将曲边梯形分割成一些小的曲边梯形, 每个小曲边梯形都用一个等宽的小矩形代替, 每个小曲边梯形的面积都近似地等于小矩形的面积, 则所有小矩形面积的和就是曲边梯形面积的近似值。
(1) 用分点a=x0<x1<x2< × × ×<xn-1<xn =b把区间[a, b]分成n个小区间,
记∆xi=xi-xi-1 (i=1, 2, × × × , n).
(2)任取
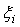 Î[xi-1, xi], 以[xi-1, xi]为底的小曲边梯形的面积可近似为 Î[xi-1, xi], 以[xi-1, xi]为底的小曲边梯形的面积可近似为
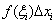 (i=1, 2, × × × , n); 所求曲边梯形面积A的近似值为 (i=1, 2, × × × , n); 所求曲边梯形面积A的近似值为
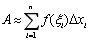 . .
(3)记l=max{x1, x2,× × ×, xn }, 曲边梯形面积的精确值为
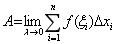 . .
2. 求变速直线运动的路程
设物体作直线运动, 已知速度v=v(t)是时间间隔[T 1, T 2]上t的连续函数, 且v(t)³0, 计算在这段时间内物体所经过的路程S 。
(1)用分点T1=t0<t1<t2<× × ×<t n-1<tn=T2把时间间隔[T 1 , T 2]分成n个小时间段,记ti =ti-ti-1 (i=1, 2, × × × , n)。
(2)任取tiÎ[ti-1, ti], 在时间段[ti-1, ti]内物体所经过的路程可近似为v(ti)Dti (i=1, 2, × × × , n); 所求路程S 的近似值为
 。 。
(3)记l=max{t1, t2,× × ×,tn}, 所求路程的精确值为
 。 。
二、定积分定义
抛开上述问题的具体意义, 抓住它们在数量关系上共同的本质与特性加以概括, 就抽象出下述定积分的定义.
1.定义 设函数
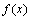 在[a, b]上有界, 用分点a=x0<x1<x2< ×××<xn-1<xn=b把[a, b]分成n个小区间: [x0, x1], [x1, x2], × × ×, [xn-1, xn] , 记Dxi=xi-xi-1(i=1, 2,× × ×, n)。任取 在[a, b]上有界, 用分点a=x0<x1<x2< ×××<xn-1<xn=b把[a, b]分成n个小区间: [x0, x1], [x1, x2], × × ×, [xn-1, xn] , 记Dxi=xi-xi-1(i=1, 2,× × ×, n)。任取
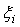 Î[xi-1, xi] (i=1, 2,× × ×, n), 作和 Î[xi-1, xi] (i=1, 2,× × ×, n), 作和
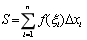 . .
记l=max{x1, x2,× × ×, xn}, 如果当l®0时, 上述和式的极限存在, 且极限值与区间[a, b]的分法和
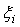 的取法无关, 则称这个极限为函数 的取法无关, 则称这个极限为函数
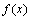 在区间[a, b]上的定积分, 记作 在区间[a, b]上的定积分, 记作
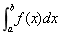 , 即 , 即
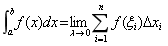 。 。
2.定积分的几何意义
在区间[a, b]上, 当
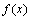 ³0时, 积分 ³0时, 积分
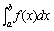 在几何上表示由曲线y= 在几何上表示由曲线y=
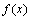 、两条直线x=a、x=b 与x轴所围成的曲边梯形的面积;当f(x)£0时, 由曲线y = 、两条直线x=a、x=b 与x轴所围成的曲边梯形的面积;当f(x)£0时, 由曲线y =
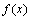 、两条直线x=a、x=b 与x轴所围成的曲边梯形位于x轴的下方, 定义分在几何上表示上述曲边梯形面积的负值; 、两条直线x=a、x=b 与x轴所围成的曲边梯形位于x轴的下方, 定义分在几何上表示上述曲边梯形面积的负值;


 . .
当
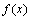 既取得正值又取得负值时, 函数 既取得正值又取得负值时, 函数
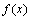 的图形某些部分在x轴的上方, 而其它部分在x轴的下方. 如果我们对面积赋以正负号, 在x轴上方的图形面积赋以正号, 在x轴下方的图形面积赋以负号, 则在一般情形下, 定积分 的图形某些部分在x轴的上方, 而其它部分在x轴的下方. 如果我们对面积赋以正负号, 在x轴上方的图形面积赋以正号, 在x轴下方的图形面积赋以负号, 则在一般情形下, 定积分
 的几何意义为: 它是介于x轴、函数f(x)的图形及两条直线x=a、x=b之间的各部分面积的代数和. 的几何意义为: 它是介于x轴、函数f(x)的图形及两条直线x=a、x=b之间的各部分面积的代数和.
三、定积分的性质
性质1 函数的和(差)的定积分等于它们的定积分的和(差) 即
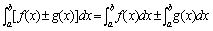 . .
性质2 被积函数的常数因子可以提到积分号外面 即
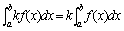 . .
性质3如果将积分区间分成两部分 则在整个区间上的定积分等于这两部分区间上定积分之和,即
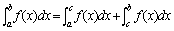 . .
这个性质表明定积分对于积分区间具有可加性.
性质4 如果在区间[a b]上
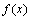 º1 则 º1 则
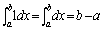 . .
性质5 如果在区间[a, b]上
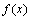 ³0, 则 ³0, 则
 (a<b). (a<b).
性质6 (定积分估值定理) 设M 及m 分别是函数
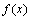 在区间[a, b]上的最大值及最小值, 则 在区间[a, b]上的最大值及最小值, 则
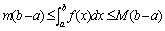 ,(a<b)。 ,(a<b)。
性质7 (定积分中值定理) 如果函数
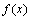 在闭区间[a, b]上连续, 则在积分区间[a,b]上至少存在一个点,使下式成立: 在闭区间[a, b]上连续, 则在积分区间[a,b]上至少存在一个点,使下式成立:
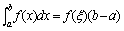 . ------积分中值公式. . ------积分中值公式.
|
思政要素
切入点
|
1.本节主要介绍了微积分理论中的定积分概念及其性质,通过求曲边梯形的面积实例总结出定积分的定义。在介绍曲边梯形的面积时,引入以平代曲的辩证哲学思想,激发学生的学习兴趣,培养学生的应用意识和解决实际问题的能力。
2.定积分的概念产生于两类科学问题:第一类是已知加速度函数求瞬时速度和路程,第二类是求曲线长、曲线围成的面积、曲面围成的体积等问题。这些问题的共性是涉及不恒定量的求解,可以用“化整为零→以直代曲→积零为整”的思路来解决,这就是定积分的思想。在讲授定积分的概念时不仅要让学生体会抽象概念的形成过程,清晰认识到数学来源于实际,而且还要让学生明白再复杂的事情都是由简单的事情组合起来的,需要我们用智慧去分解,理性平和地去做事。
3.在讲授定积分的概念和性质时,将不定积分和定积分的概念进行对比,揭示其中蕴含的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。
|
教学策略
|
案例教学、讨论教学、混合式教学
|
三、案例实施
一、实施过程
1.求曲边梯形的面积时,引入“以直代曲”的哲学思想。
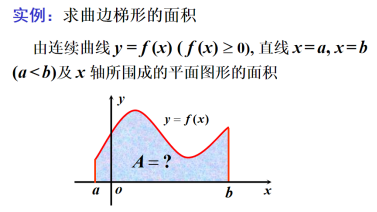
思想方法:以直代曲。将曲边梯形分割成一些小的曲边梯形, 每个小曲边梯形都用一个等宽的小矩形代替, 每个小曲边梯形的面积都近似地等于小矩形的面积, 则所有小矩形面积的和就是曲边梯形面积的近似值。
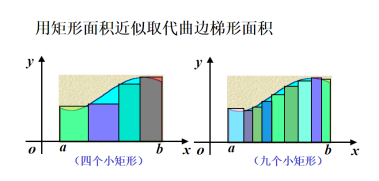
(1)用分点a=x0<x1<x2< × × ×<xn-1<xn =b把区间[a, b]分成n个小区间, 记∆xi=xi-xi-1 ,(i=1, 2, × × × , n).
(2)任取
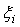 Î[xi-1, xi], 以[xi-1, xi]为底的小曲边梯形的面积可近似为 Î[xi-1, xi], 以[xi-1, xi]为底的小曲边梯形的面积可近似为
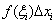 (i=1, 2, × × × , n); 所求曲边梯形面积A的近似值为 (i=1, 2, × × × , n); 所求曲边梯形面积A的近似值为
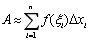 . .
(3)记l=max{x1, x2,× × ×, xn }, 曲边梯形面积的精确值为
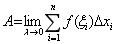 . .
求曲边梯形面积过程中,采用了“化整为零→以直代曲→积零为整”的思路来解决,引入了以直代曲的哲学思想,这也是定积分的思想。讲授定积分的思想不仅要让同学体会抽象概念的形成过程,清晰认识到数学来源于实际,而且还要明白再复杂的事情都是由简单的事情组合起来的,需要我们用智慧去分解,理性平和地去做事。
求曲边梯形面积的过程中所使用的以直代曲的思想方法,其实是中国古代数学的成果,在刘徽的割圆术中就蕴含着化圆为方、以直代曲的思想。中国是一个有着五千年文明历史的泱泱大国,数学发展的成果也是五千年灿烂文化的一部分,是我们民族、文化传承的宝贵财富之一。以此鼓励同学们要刻苦学习,努力成为中国传统文化的传承者、创新者。
2.讲授定积分的定义时,将不定积分和定积分的概念进行对比。
在介绍了求曲边梯形的面积和求变速直线运动物体的路程两个实例后,抛开上述问题的具体意义, 抓住它们在数量关系上共同的本质与特性加以概括, 就抽象出下述定积分的定义。
定义:设函数
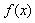 在[a, b]上有界, 用分点a=x0<x1<x2< ×××<xn-1<xn=b把[a, b]分成n个小区间: [x0, x1], [x1, x2], × × ×, [xn-1, xn] , 记xi=xi-xi-1(i=1, 2,× × ×, n)。任取 在[a, b]上有界, 用分点a=x0<x1<x2< ×××<xn-1<xn=b把[a, b]分成n个小区间: [x0, x1], [x1, x2], × × ×, [xn-1, xn] , 记xi=xi-xi-1(i=1, 2,× × ×, n)。任取
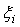 Î[xi-1, xi] (i=1, 2,× × ×, n), 作和 Î[xi-1, xi] (i=1, 2,× × ×, n), 作和
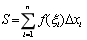 . .
记l=max{x1, x2,× × ×, xn}, 如果当l®0时, 上述和式的极限存在, 且极限值与区间[a, b]的分法和
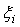 的取法无关, 则称这个极限为函数 的取法无关, 则称这个极限为函数
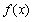 在区间[a, b]上的定积分, 记作 在区间[a, b]上的定积分, 记作
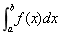 , 即 , 即
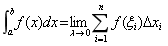 。 。
在讲授定积分的概念的同时,将上一章刚刚学过的不定积分和定积分的概念进行对比,揭示其中蕴含的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。
二、取得成效
求曲边梯形的面积是没有现成的公式可用,教学时由老师带领学生一步步探索,利用“化整为零→以直代曲→积零为整”的方法,使学生体会到了抽象概念的形成过程,学会探索。定积分的定义蕴含着以直代曲化整为零的思想,使学生体会到复杂的事情可以用智慧去分解,理性平和做事。在中国古代数学圆周率的研究中已经蕴含着化圆为方、以直代曲的思想,领先世界一千多年。这些辉煌成果无疑可以激发学生的民族和文化的自豪感和认同感,激励他们成为中国传统文化的传承者、创新者。
三、教学反思
本节课的思政案例把教学内容和哲学、创新、人文精神结合起来,加深了学生的思想深度,使学生的数学学习水平和思想政治水平同时得到提高,有助于学生形成正确的世界观、价值观、人生观,从而为教学水平的提高、为高层次人才的培养起到推动作用。
|
案例3:数列极限的定义
一、基本信息
课程名称
|
《高等数学》A2
|
授课教师/职称
|
李明哲、徐亚兰、毕淑娟、曹辉/副教授;
朱莉、盛晓娜、王永红/讲师
|
课程类型
|
专业教育课程
|
课程性质
|
þ必修 ¨选修
|
案例学时/总学时
|
2/160
|
授课对象及人数
|
计算机、软件工程、土木、城地21级/485人
|
教学方式
|
þ线下 ¨线上 ¨线上线下混合式
|
二、案例设计
本次课程目标:
1.掌握数列极限的“
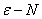 ”定义以及它的几何意义, ”定义以及它的几何意义,
2.掌握收敛数列的性质。
思政育人目标:
数列极限概念的教学,将课程思政元素融入教学与学习过程中,最终使得学生在有效的教学情境中达到深刻理解数列极限的概念、领会极限的思想的目的。增强学生的文化自信和民族自豪感,激发学生的爱国情怀和追求科学真理的动力。
|
案例教学
内容
|
一、数列极限的定义
1.一个实际问题:如可用渐近的方程法求圆的面积?
设有一圆, 首先作内接正四边形, 它的面积记为A1;再作内接正八边形, 它的面积记为A2;再作内接正十六边形, 它的面积记为A3;如此下去, 每次边数加倍, 一般把内接正8×2n-1边形的面积记为An . 这样就得到一系列内接正多边形的面积:
A1, A2, A3, × × × , An, × × ×
设想n 无限增大(记为n®¥, 读作n 趋于穷大), 即内接正多边形的边数无限增加, 在这个过程中, 内接正多边形无限接近于圆, 同时An 也无限接近于某一确定的数值, 这个确定的数值就理解为圆的面积. 这个确定的数值在数学上称为上面有次序的数(数列) A1, A2, A3, × × × , An, × × ×当n ®¥时的极限.
2.数列的概念:如果按照某一法则, 使得对任何一个正整数n 有一个确定的数xn , 则得到一列有次序的数
x1, x2, x3, × × × , xn , × × ×
这一列有次序的数就叫做数列, 记为{xn}, 其中第n 项xn 叫做数列的一般项.
数列的几何意义:数列{xn}可以看作数轴上的一个动点, 它依次取数轴上的点x1, x2, x3, × × × , xn , × × ×
数列与函数:数列{xn}可以看作自变量为正整数n 的函数: xn=f (n), 它的定义域是全体正整数.
3. 数列的极限
数列的极限的通俗定义:对于数列{xn}, 如果当n 无限增大时, 数列的一般项xn无限地接近于某一确定的数值a, 则称常数a 是数列{xn}的极限, 或称数列{xn}收敛a . 记为
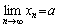 . 如果数列没有极限, 就说数列是发散的. . 如果数列没有极限, 就说数列是发散的.
例如
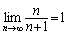 , ,
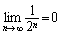 , ,
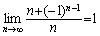 ; 而{2n}, { (-1)n+1}, 是发散的 ; 而{2n}, { (-1)n+1}, 是发散的
对无限接近的刻划:xn无限接近于a 等价于|xn-a |无限接近于0。
4.极限的精确定义:
定义 如果数列{xn}与常a 有下列关系:对于任意给定的正数,不论它多么小, 总存在正整数N , 使得对于n >N 时的一切xn, 不等式
|xn-a |<e e
都成立, 则称常数a 是数列{xn}的极限, 或者称数列{xn}收敛于a , 记为
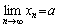 或xn®a (n®¥). 或xn®a (n®¥).
如果数列没有极限, 就说数列是发散的.
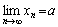 Û"e >0, $NÎN+, 当n>N时, 有|xn-a|<e . Û"e >0, $NÎN+, 当n>N时, 有|xn-a|<e .
5. 数列极限的几何解释:
二、收敛数列的性质
定理1(极限的唯一性) 数列{xn}不能收敛于两个不同的极限.
证明: 假设同时有
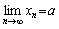 及 及
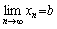 , 且a<b. , 且a<b.
按极限的定义, 对于
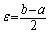 >0, 存在充分大的正整数N, 使当n>N时, >0, 存在充分大的正整数N, 使当n>N时,
同时有
|xn-a|<
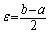 及|xn-b|< 及|xn-b|<
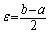 , ,
因此同时有
 及 及
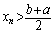 , ,
这是不可能的. 所以只能有a=b.
数列的有界性:
对于数列{xn},如果存在着正数M,使得对一切xn都满足不等式|xn|£M,则称数列{xn}是有界的; 如果这样的正数M不存在,就说数列{xn}是无界的
定理2(收敛数列的有界性) 如果数列{xn}收敛, 那么数列{xn}一定有界.
证明: 设数列{xn}收敛, 且收敛于a, 根据数列极限的定义, 对于e =1, 存在正整数N, 使对于n>N 时的一切xn , 不等式|xn-a|<1都成立. 于是当n>N时,
|xn|=|(xn -a)+a| £| xn-a|+|a|<1+|a|.
取M=max{|x 1|, |x 2|, × × ×, |x N |, 1+| a |}, 那么数列{xn}中的一切xn都满足不等式|xn|£ M。这就证明了数列{xn}是有界的.
定理3(收敛数列的保号性) 如果数列{xn}收敛于a, 且a>0(或a<0), 那么存在正整数N, 当n>N时, 有xn>0(或xn<0).
|
思政要素
切入点
|
1.通过一些古诗、歌曲、绘画等形象的案例去感受“极限”,如: 李白的古诗《黄鹤楼送孟浩然之广陵》中的第三句话“孤帆远影碧空尽,唯见长江天际流。”,形象地描述了小船无限的变化过程.
2.讲授极限概念时,春秋时期《墨经》中“穷,或有前,不容尺也”;战国时期《庄子天下篇》中“一尺之锤,日取其半,万世不竭”;魏晋时期《九章算术注》中刘徽的割圆术“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”。这些都是朴素直观的对极限思想的理解。刘徽对圆面积公式的证明,被公认为世界数学史上首次将极限思想和无穷小分割方法引入数学证明。南北朝时期的祖冲之在其基础上将圆周率精确到小数点后7位,比欧洲人早一千多年。这些史料不仅加深对极限概念的理解,能掌握概念本质,而且增强学生的文化自信和民族自豪感。
3.深刻理解数列极限定义,解释定义中ε的双重作用,绝对任意性和相对固定性。定义中的N具有相应性,N不唯一.
|xn- a|<ε是一个条件不等式,只需 N 之后的所有项满足不等式.定义中的 N 虽然很大,但也是有限的数,认知有限和无限的本质区别,隐喻滴水穿石,愚公移山的精神,调动学生学习兴趣。
4.举个有趣的例子,
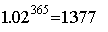 , ,
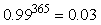 ,这个例子说明积跬步以致千里,积怠惰以致深渊,警示学生每天多努力一点,锲而不舍,在教学中渗透育人思想,传播正能量,构建正确的社会主义核心价值观。 ,这个例子说明积跬步以致千里,积怠惰以致深渊,警示学生每天多努力一点,锲而不舍,在教学中渗透育人思想,传播正能量,构建正确的社会主义核心价值观。
|
教学策略
|
案例教学、讨论教学、混合式教学
|
三、案例实施
一、实施过程
1.直观体验极限思想
在讲授数列极限的概念时,首先指出极限是刻画事物的变化趋势的工具。事先每个学生准备长约 20 cm 的绳子,第一次用剪刀截取它的一半,第二次再截取一半,继续下去,那么这根绳子永远也截取不完。


战国时期《庄子天下篇》中“一尺之锤,日取其半,万世不竭”体现了极限思想,通过学生动手截取绳子实际操作,体验截取绳子中极限的思想,加深了对极限思想的理解。
2. PPT 展示
画一个圆,做一个内接正六边形,设其面积为 A1,再做一个内接正十二边形,面积为 A2,再做内接正二十四边形,面积为 A3,内接正6×(2n - 1) 边形,面积为 An,通过 PPT 演示,学生可直观看到,当 n 越来越大时,An 越来越接近于圆的面积。
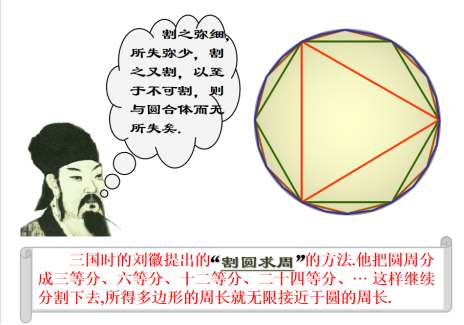

魏晋时期《九章算术注》中刘徽的割圆术“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”。这些都是朴素直观的对极限思想的理解。刘徽对圆面积公式的证明,被公认为世界数学史上首次将极限思想和无穷小分割方法引入数学证明。南北朝时期的祖冲之在其基础上将圆周率精确到小数点后7位,比欧洲人早一千多年。这些史料不仅加深对极限概念的理解,能掌握概念本质,而且增强学生的文化自信和民族自豪感。
3.通过古诗、绘画形象的案例去感受“极限”


李白的古诗《黄鹤楼送孟浩然之广陵》中的第三句话“孤帆远影碧空尽,唯见长江天际流。”,形象地描述了小船由近及远至无限的变化过程。
3. 举一个有趣的例子


利用这个答案告诉学生,积跬步以致千里,积怠惰以致深渊。警示学生每天多努力一点,锲而不舍,一年后会得到更多的收获。在教学中渗透育人思想,传播正能量,构建正确的社会主义核心价值观。
4. 深刻理解数列极限定义,解释定义中ε的双重作用,绝对任意性和相对固定性。
定义中的N具有相应性,N不唯一,|xn- a|<ε是一个条件不等式,只需 N 之后的所有项满足不等式。定义中的 N 虽然很大,但也是有限的数,认知有限和无限的本质区别,隐喻滴水穿石,愚公移山的精神,调动学生学习兴趣。
二、取得成效
数列极限概念的教学,将课程思政元素融入教学与学习过程中,最终使得学生在有效的教学情境中达到深刻理解数列极限的概念、领会极限的思想的目的,从而完成学生对知识的感知阶段、理性认识阶段、概括阶段和运用阶段四个阶段的升华。概念的引入设计了学生动手实践环节,即体验学习教学法,使学生亲自参与知识的建构,亲历过程并在过程中体验知识。介绍魏晋时期数学家的刘徽的“割圆术”,既是知识层面上的教育,又是正确价值观的引领,使学生感受中国两千年文化底蕴,激发学生的民族自豪感和文化自信。在特定的教学情景中渗透数学思想方法,从特殊到一般给出数列极限定义,数形结合主观感悟数列极限的几何特征本质,以学生发展为目标,注重学生学到了什么,促进数学核心素养的形成。
三、教学反思
《高等数学》作为高校理工科重要的专业基础课程,如何进行思想政治教育,实现课程思政与思想课程同向同行,是一个重要的研究课题。
本节极限概念教学中,将数学史、数学思想和历史文化中蕴含的思政元素通过“植入”教学模式融入课程教学,取得了不错的教学效果。这些课程思政映射点把科学内容和哲学、美学、创新、人文精神结合起来,使学生的专业学习水平和思想政治水平同时得到提高,有助于大学生形成正确的世界观、价值观、人生观。思政因子植入教学,要善于讲好“数学故事”,隐藏动机,把深刻的数学思想、抽象的数学概念和定理,转化为生动的语言和案例,在教学过程中自然而然插入思政元素。过于明显和突兀的插入会让人感觉过于生硬,起不到原有的教育作用。只有跳出传统教学框架,着重挖掘贴近生活能触动学生兴趣点的思政素材,让思政理念贯穿学习始终,将其和数学知识融会贯通,在“润物无声”中构建符合社会主义核心价值的“数学观”,才能让学生喜闻乐见、易于接受,真正做到“立德树人”。
|
案例4:函数的极值与最值
一、基本信息
课程名称
|
《高等数学》A2
|
授课教师/职称
|
李明哲、徐亚兰、毕淑娟、曹辉/副教授;
朱莉、盛晓娜、王永红/讲师
|
课程类型
|
专业教育课程
|
课程性质
|
þ必修 ¨选修
|
案例学时/总学时
|
2/160
|
授课对象及人数
|
计算机、软件工程、土木、城地21级/485人
|
教学方式
|
¨线下 ¨线上 ¨线上线下混合式
|
二、案例设计
本次课程目标:
1.理解函数极值的概念,掌握函数的极值的求法。
2.会求最大值、最小值及解决相应的的实际应用问题。
思政育人目标:
在讲解极值这个知识点的时候,利用极大值极小值的概念使学生感悟到人生就像连绵不断的曲线,起起落落是必经之路,是成长的需要,要做到跌入低谷不气馁,甘于平淡不放任。要学会用运动的观点看待问题,低谷与顶峰只是我们人生路上的一个转折点。要认识事物的真相与全貌,必须超越狭小的范围,摆脱主观成见。
|
案例教学
内容
|
§3.5 函数的极值与最大值最小值
一、函数的极值及其求法
1.极值的定义
定义 设函数f(x)在区间(a, b)内有定义, x0Î(a, b). 如果在x0的某一去心邻域内有f(x)<f(x0), 则称f(x0)是函数 f(x)的一个极大值; 如果在x0的某一去心邻域内有f(x)>f(x0), 则称f(x0)是函数f(x)的一个极小值。函数的极大值与极小值统称为函数的极值, 使函数取得极值的点称为极值点.
注:(1)函数的极大值和极小值概念是局部性的. 如果f(x0)是函数f(x)的一个极大值, 那只是就x0 附近的一个局部范围来说, f(x0)是f(x)的一个最大值; 如果就f(x)的整个定义域来说, f(x0)不一定是最大值. 关于极小值也类似.
(2)极值与水平切线的关系: 在函数取得极值处, 曲线上的切线是水平的. 但曲线上有水平切线的地方, 函数不一定取得极值。
定理1 (必要条件)设函数f(x)在点x0 处可导, 且在x0 处取得极值, 那么这函数在x0 处的导数为零, 即f ¢(x0)=0.
驻点: 使导数为零的点(即方程f ¢(x) = 0的实根)叫函数f(x)的驻点. 定理1就是说: 可导函数f(x)的极值点必定是函数的驻点. 但的过来, 函数f(x)的驻点却不一定是极值点。考察函数f(x)=x3在x=0处的情况。
定理2(第一种充分条件)设函数f(x)在点x0的一个邻域内连续, 在x0的左右邻域内可导,
(1) 如果在x0的某一左邻域内f ¢(x)>0, 在x0的某一右邻域内f ¢(x)<0, 那么函数f(x)在x0处取得极大值;
(2) 如果在x0的某一左邻域内f ¢(x)<0, 在x0的某一右邻域内f ¢(x)>0, 那么函数f(x)在x0处取得极小值;
(3)如果在x0的某一邻域内f ¢(x)不改变符号, 那么函数f(x)在x0处没有极值。
确定极值点和极值的步骤:
(1) 求出导数f ¢(x);
(2) 求出f(x)的全部驻点和不可导点;
(3) 列表判断(考察f ¢(x)的符号在每个驻点和不可导点的左右邻近的情况, 以便确定该点是否是极值点, 如果是极值点, 还要按定理2确定对应的函数值是极大值还是极小值);
(4) 确定出函数的所有极值点和极值
例1求函数
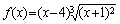 的极值. 的极值.
定理3 (第二种充分条件) 设函数f(x)在点x0处具有二阶导数且f ¢(x0)=0, f ¢¢(x0)¹0, 那么
(1)当f ¢¢(x0)<0时, 函数f(x)在x0处取得极大值;
(2)当f ¢¢(x0)>0时, 函数f(x)在x0处取得极小值。
二、最大值最小值问题
在工农业生产、工程技术及科学实验中, 常常会遇到这样一类问题: 在一定条件下, 怎样使“产品最多”、“用料最省”、“成本最低”、“效率最高”等问题, 这类问题在数学上有时可归结为求某一函数(通常称为目标函数)的最大值或最小值问题.
1. 极值与最值的关系:
设函数f(x)在闭区间[a, b]上连续, 则函数的最大值和最小值一定存在. 函数的最大值和最小值有可能在区间的端点取得, 如果最大值不在区间的端点取得, 则必在开区间(a, b)内取得, 在这种情况下, 最大值一定是函数的极大值. 因此, 函数在闭区间[a, b]上的最大值一定是函数的所有极大值和函数在区间端点的函数值中最大者. 同理, 函数在闭区间[a, b]上的最小值一定是函数的所有极小值和函数在区间端点的函数值中最小者.
2. 最大值和最小值的求法:
设f(x)在(a, b)内的驻点和不可导点(它们是可能的极值点)为x1, x2, × × × , xn, 则比较 f(a), f(x 1), × × × , f(x n), f(b)的大小, 其中最大的便是函数f(x)在[a, b]上的最大值, 最小的便是函数f(x)在[a, b]上的最小值.
例3求函数f(x)=|x2-3x+2|在[-3, 4]上的最大值与最小值.
|
思政要素
切入点
|
1.在讲解函数极大值极小值的概念时,引入北宋文学家苏轼的“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中”的诗句,这首诗描绘的是庐山随着观察者角度不同,呈现出不同的样貌。高等数学中函数极值这个知识点,数形结合后画出来的图形,就像庐山的山岭一样连绵起伏,极大值在山顶取得,极小值则是出现在山谷。
2.通过《题西林壁》这首诗引入极值的概念,会给抽象的数学课堂注入一缕诗情画意。在讲解极值这个知识点的时候,不仅要教会学生求.函数的极值点与极值。同时还可以让学生感悟。人生就像连绵不断的曲线,起起落落是必经之路,是成长的需要,跌入低谷不气馁,甘于平淡不放任,伫立高峰不张扬,这才叫宽阔胸襟。要学会用运动的观点看待问题,低谷与顶峰只是我们人生路上的一个转折点。要认识事物的真相与全貌,必须超越狭小的范围,摆脱主观成见。
3.在讲授函数的极值问题时,需要强调极值和最值的定义。极值是局部的,只与其附近点上的函数值有关;而最值是整体的,与所有点上的函数值有关。极值好比井底之蛙,坐井观天;而最值放眼世界,有大局观。这可以促使学生努力开阔自己的学习视野,站在更高的角度胸怀祖国、放眼世界。
|
教学策略
|
讨论教学、混合式教学
|
三、案例实施
一、实施过程
1.利用古诗词,形象刻画极值的概念。
极值的定义:设函数f(x)在区间(a, b)内有定义, x0Î(a, b)。如果在x0的某一去心邻域内有f(x)<f(x0), 则称f(x0)是函数 f(x)的一个极大值; 如果在x0的某一去心邻域内有f(x)>f(x0), 则称f(x0)是函数f(x)的一个极小值。函数的极大值与极小值统称为函数的极值。
本节课主要介绍极值的概念和求法。在介绍极大值、极小值的概念时,引入北宋文学家苏轼的诗句“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中”。《题西林壁》这首诗描绘的是庐山随着观察者角度不同,呈现出不同的样貌。高等数学中函数的极值这个知识点,数形结合后画出来的图形,就像庐山的山岭一样连绵起伏,极大值在山顶取得,极小值则是出现在山谷。

通过《题西林壁》这首诗的引入,给抽象的数学课堂注入了一缕诗情画意。在讲解极值这个知识点的时候,不仅要教会学生极值的概念和求函数的极值点与极值的方法,同时还要让学生感悟人生就像连绵丕断的曲线,起起落落是必经之路,是成长的需要,跌入低谷不气馁,甘于平淡不放任,伫立高峰不张扬,这才叫宽阔胸襟。还要提示学生学会用运动的观点看待问题,低谷与顶峰只是我们人生路上的一个转折点。要认识事物的真相与全貌,必须超越狭小的范围,摆脱主观成见。
2.比较函数的极值和最值的区别与联系,加以引申。
在讲授函数的极值问题时,需要强调极值和最值的定义。极值是局部的,只与其附近点上的函数值有关;而最值是整体的,与所有点上的函数值有关。可以引申为极值好比井底之蛙,坐井观天;而最值放眼世界,有大局观。这可以促使学生努力开阔自己的学习视野,站在更高的角度胸怀祖国、放眼世界。
二、取得成效
数学知识本是枯燥的,但是用喜闻乐见的方式就会使学生感到有趣,从而提高学习的兴趣。本节在介绍极值的概念时,引入北宋文学家苏轼的诗《题西林壁》,数形结合后画出来的图形,就像庐山的山岭一样连绵起伏,直观地展示了所学的极值概念,给抽象的数学课堂注入一缕诗情画意,将诗词与
数学内容有机结合,融入课堂教学,培养学生的爱国情怀和人文精神。
同时引导学生感悟到:人生就像连绵不断的曲线,起起落落是必经之路,是成长的需要,跌入低谷不气馁,甘于平淡不放任,伫立高峰不张扬,这才叫胸怀。在介绍极值与最值概念的区别于联系时,引导学生感悟到要用发展的眼光看待问题,低谷与顶峰只是我们人生路上的一个转折点。要认识事物的真相与全貌,必须超越狭小的范围,摆脱主观成见。
本节课将思政元素悄无声息地融入到教学中,使学生通过体验式思考实现了情感共鸣和思想认同。
三、教学反思
本节课结合课程的特点充分发掘思政元素,选择合适的教学手段和方法,寻找适合的思政点融入教学,使思政教育的因子无痕地融入了课程教学中,同时用具有正能量、积极向上的思政教育给予学生的世界观、人生观、价值观以积极正面的引导,实现知识传授与价值引导、科学素养与人文精神的有机融合,达到循序渐进、润物无声、潜移默化的思政育人效果。
需要注意的是课程思政要点到为止,不能喧宾夺主,不能影响正常的教学进度,否则容易引起学生的反感。
|
案例5:函数的连续性与间断点
一、基本信息
课程名称
|
《高等数学》A2
|
授课教师/职称
|
李明哲、徐亚兰、毕淑娟、曹辉/副教授;
朱莉、盛晓娜、王永红/讲师
|
课程类型
|
专业教育课程
|
课程性质
|
þ必修 ¨选修
|
案例学时/总学时
|
2/160
|
授课对象及人数
|
计算机、软件工程、土木、城地21级/485人
|
教学方式
|
¨线下 ¨线上 þ线上线下混合式
|
二、案例设计
本次课程目标:
1.理解掌握函数连续、间断的概念
2.能求函数的间断点,会判断掌握间断点的类型
思政育人目标:
1.讲授函数连续的概念时,通过引入拔苗助长的故事,使学生明白学生学习或做事不能急功近利,要踏实肯干。
2.函数连续性与间断性是一对相反的概念,通过对比概念,使学生理解蕴含的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。
|
案例教学
内容
|
§1.8 函数的连续性与间断点
一、函数的连续性
1.变量的增量:
设变量u从它的一个初值u1变到终值u2, 终值与初值的差u2-u1就叫做变量u的增量, 记作Du , 即Du =u2-u1。
设函数y=f(x)在点x0的某一个邻域内是有定义的. 当自变量x 在这邻域内从x0变到x0+Dx时, 函数y相应地从f(x0)变到f(x0+Dx), 因此函数y的对应增量为Dy= f(x0+Dx)- f(x0)。
2.函数连续的定义
设函数y=f(x)在点x0 的某一个邻域内有定义, 如果当自变量的增量Dx =x-x0 趋于零时, 对应的函数的增量Dy= f(x0+Dx)- f(x0 )也趋于零, 即
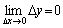 , 或 , 或
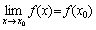 , ,
那么就称函数y=f(x)在点x0 处连续.
注: ①
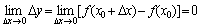
②设x=x0+Dx, 则当Dx®0时, x®x0, 因此
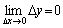 Û Û
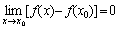 Û Û
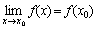 . .
函数连续的等价定义:设函数y=f(x)在点x0的某一个邻域内有定义, 如果对于任意给定的正数e , 总存在正数d , 使得对于适合不等式|x-x0|<d 的一切x, 对应的函数值f(x)都满足不等式|f(x)-f(x0)|<e , 那么就称函数y=f(x)在点x0处连续.
3.左右连续性:
如果
 , 则称y=f(x)在点 , 则称y=f(x)在点
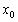 处左连续. 处左连续.
如果
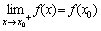 , 则称y=f(x)在点 , 则称y=f(x)在点
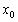 处右连续. 处右连续.
左右连续与连续的关系:
函数y=f(x)在点x0处连续Û函数y=f(x)在点x0处左连续且右连续.
函数在区间上的连续性:
在区间上每一点都连续的函数, 叫做在该区间上的连续函数, 或者说函数在该区间上连续. 如果区间包括端点, 那么函数在右端点连续是指左连续, 在左端点连续是指右连续。
连续函数举例:
1. 如果f(x)是多项式函数, 则函数f(x)在区间(-¥, +¥)内是连续的.
这是因为, f(x)在(-¥, +¥)内任意一点x0处有定义, 且
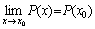 . .
2. 函数
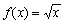 在区间[0, +¥)内是连续的. 在区间[0, +¥)内是连续的.
3. 函数y=sin x 在区间(-¥, +¥)内是连续的.
4. 函数y=cos x 在区间(-¥, +¥)内是连续的.
二、函数的间断点
1.间断定义
设函数f(x)在点x0的某去心邻域内有定义. 在此前提下, 如果函数f(x)有下列三种情形之一:
(1)在x0没有定义;
(2)虽然在x0有定义, 但
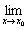 f(x)不存在; f(x)不存在;
(3)虽然在x0有定义且
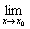 f(x)存在, 但 f(x)存在, 但
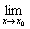 f(x)¹f(x0); f(x)¹f(x0);
则函数f(x)在点x0为不连续, 而点x0称为函数f(x)的不连续点或间断点。
2.间断点的分类
通常把间断点分成两类:如果x0是函数f(x)的间断点, 但左极限f(x0-0)及右极限f(x0+0)都存在, 那么x0称为函数f(x)的第一类间断点;不是第一类间断点的任何间断点,称为第二类间断点;在第一类间断点中, 左、右极限相等者称为可去间断点, 不相等者称为跳跃间断点;无穷间断点和振荡间断点显然是第二间断点。
例1. 正切函数y=tan x在
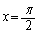 处没有定义, 所以点 处没有定义, 所以点
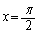 是函数tan x的间断点。 是函数tan x的间断点。
因为
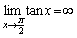 , 故称 , 故称
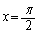 为函数tan x的无穷间断点。 为函数tan x的无穷间断点。
例2. 函数
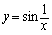 在点x=0没有定义, 所以点x=0是函数 在点x=0没有定义, 所以点x=0是函数
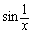 的间断点。 的间断点。
当x®0时, 函数值在-1与+1之间变动无限多次, 所以点x=0称为函数
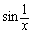 的振荡间断点. 的振荡间断点.
例3. 函数
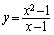 在x=1没有定义, 所以点x=1是函数的间断点. 在x=1没有定义, 所以点x=1是函数的间断点.
|
思政要素
切入点
|
1.讲授函数连续的概念时,通过引入拔苗助长的故事,揭示辩证唯物主义中量变到质变的规律,使学生明白学生学习或做事情不能急功近利,要踏实肯干。
2.函数连续性与间断性是一对相反的概念,在这里植入数学哲学和数学文化基因。对比函数的连续性与间断性概念,解释蕴含其中的的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。
|
教学策略
|
运用讨论教学、混合式教学法
|
三、案例实施
一、实施过程
1.发动学生寻找生活中的连续现象,抽象出连续概念。
自然界的许多现象,如气温的变化、河水的流动、植物的生长等都是连续地变化着的。这种现象在函数关系上的反映,就是函数的连续性。例如就气温的变化来看,当时间变动很微小时,气温的变化也很微小,这种特点就是所谓连续性。在介绍函数连续的概念前,发动学生列举生活中的连续现象。



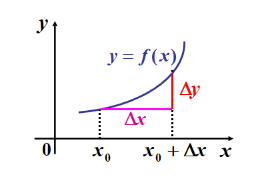
函数连续的定义
设函数y=f(x)在点x0 的某一个邻域内有定义, 如果当自变量的增量Dx =x-x0 趋于零时, 对应的函数的增量Dy= f(x0+Dx)- f(x0 )也趋于零, 即
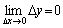 , 或 , 或
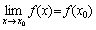 ,那么就称函数y=f(x)在点x0 处连续. ,那么就称函数y=f(x)在点x0 处连续.
给出函数连续的概念后,引入拔苗助长的成语典故,揭示辩证唯物主义中量变到质变的规律,使学生明白学生学习或做事情不能急功近利,要脚踏实地,一点一滴积累成长。

2.在介绍完函数的连续性,接着讲解函数的间断性时,把二者做对比。函数连续性与间断性是一对相反的概念,通过对比,解释蕴含其中的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。
二、取得成效
本节课讲授函数连续的概念时引入拔苗助长的故事,揭示了辩证唯物主义中量变到质变的规律,使学生明白学生学习或做事情不能急功近利,要踏实肯干。在对比介绍函数连续性与间断性这对相反的概念时,植入数学哲学和数学文化基因,解释蕴含其中的的矛盾的对立统一、普遍联系和否定之否定的辩证哲学规律。这些课程思政案例把科学内容和哲学、美学、创新、人文精神结合起来,使大学生的专业学习水平和思想政治水平同时得到提高,有助于大学生形成正确的世界观、价值观、人生观。
三、教学反思
育人是一个循序渐进的过程。作为数学教师,要积极更新教学理念,结合课程内容的特点充分发掘思政元素,选择合适的教学手段和方法,使思政教育的因子无痕地融入课程教学中。用具有正能量、积极向上的思政教育给予大学生的世界观、人生观、价值观以积极正面的引导,实现知识传授与价值引导、科学素养与人文精神的有融合,才能达到循序渐进、润物无声、潜移默化的思政育人效果。
|
【关闭】
|
|

