(500字以上,图文并茂)
一、实施过程
1.课程回顾
引导学生温故向量组的线性相关性
2.问题提出
本节课需介绍施瓦茨不等式:[ x , y ]2 ≤ [x , x ] [y , y ],从而介绍施瓦茨的人生经历。
施瓦茨,即法国数学家H.A.施瓦茨,1843.1.25出生,生于西里西亚(Sukesia)的赫姆斯多夫(Hermsdorf),卒于柏林。1860年进入柏林工业学院学习化学,后来受库默尔和魏尔斯特拉斯影响转而攻读数学。1864年毕业,并获哲学博士学位。1867年在哈雷大学任教授,1869年任苏黎世大学教授,1875年到哥廷根大学数学系任教。1892年接替他的老师魏尔斯特拉斯在柏林大学的教授职务。任教期间当选为普鲁士科学院和巴伐利亚科学院院士。

3.新知识点讲解及问题解决方案
定义1 设有n维向量
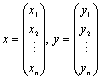 ,令[ x , y ] = x1 y1 + x2 y2 + …+ xn yn ,称[ x , y ] 为向量 x 与 y 的内积。易知内积的结果是一个实数,且[ x , y ] = xTy。 ,令[ x , y ] = x1 y1 + x2 y2 + …+ xn yn ,称[ x , y ] 为向量 x 与 y 的内积。易知内积的结果是一个实数,且[ x , y ] = xTy。
内积具有下列性质:
1、[ x , y ] = [ y , x ];
2、[λx , y ] =λ[ x,y ];
3、[ x + y , z ] = [ x , z ] + [ y , z ];
4、[ x , x ] ≥0,当且仅当x = 0 时 [ x , x ] = 0。
5、施瓦茨不等式:[ x , y ]2 ≤ [x , x ] [y , y ]。
其中 x,y,z 是为向量,
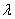 为实数。 为实数。
定义2 非负实数
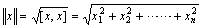 称为n维向量x的长度(范数)。 称为n维向量x的长度(范数)。
长为 1 的向量称为单位向量;若向量 x ≠0,

向量的长度具有性质:
1、非负性:
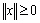 ,当且仅当 ,当且仅当
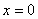 时, 时,
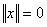 ; ;
2、齐次性:
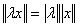 ; ;
3、三角不等式:
 。 。
如果 [ x , y ] = 0 ,那么称向量 x 与 y 正交。显然,若
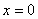 ,则x与任何向量都正交。正交向量组:一组两两正交的非零向量。 ,则x与任何向量都正交。正交向量组:一组两两正交的非零向量。
定理1 正交向量组必线性无关.
例1.已知R3中两个向量
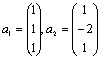 正交,试求一个非零向量 正交,试求一个非零向量
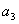 ,使 ,使
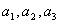 两两正交。 两两正交。
解:令
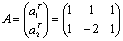 , ,
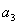 满足 满足
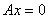 ,即 ,即
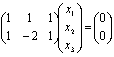
由
 ,得 ,得
 ,从而有基础解系 ,从而有基础解系
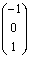 取为 取为
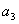 既为所求。 既为所求。
二、取得成效
通过引导学生了解施瓦茨的数学成就,涉及分析学、微分方程、几何学等领域,及与之有关联的伟大人物,如维尔斯特拉斯,埃尔米特等,他们之间良好的关系促进了科学知识的交流和发展,使同学们能在大学生活中拓宽眼界,多结交志同道合,追梦未来的人,一起探讨问题,感悟文明思想的熏陶和绽放新的思想。这些课外素材的引入能够激起学生的兴趣,课堂教学的氛围活跃,学生能积极主动和教师交流东西方文明的异同,提出所讲述知识的疑惑和个人的见解,师生的互动进一步烘托课堂的氛围。
三、教学反思
教学过程中,学生对向量及正交向量的概念理解不是特清晰,对抽象问题的理解不到位,并且学生对数学史的了解很是浅薄,很多优秀的数学家从来没有听闻过,视野相对很是狭窄。此外单纯的理论讲述并容易让学生理解,需要配合更多的实际例子关联讲授,这需要在课程准备阶段投入更多精力引入好的教学案例,以期让课堂效果达到更好。
|

